1.8 有源带通滤波器

在本教程中，我们将学习有源带通滤波器，包括其频率响应、类型、示例等更多内容。在之前的教程中，我们已经学习了带通滤波器，但该教程的设计方法基于无源元件。

带通滤波器与其他滤波器一样，也可以围绕有源元件（如晶体管和运算放大器）进行设计。如果您需要更多关于无源带通滤波器的信息，请阅读“无源带通 RC 滤波器”。

有源带通滤波器简介

带通滤波器是一种仅允许特定频率范围通过的电路。这个通带主要位于截止频率之间，分别为 $f_L$ 和 $f_H$，其中 $f_L$ 是下截止频率， $f_H$ 是上截止频率。

中心频率用 $f_c$ 表示，也被称为谐振频率或峰值频率。

$f_L$ 的值必须始终小于 $f_H$ 的值。滤波器的通带实际上就是带宽。滤波器在谐振或中心频率处的增益最大，这被称为总通带增益，用 $A_{\text{max}}$ 表示。

对于低通滤波器，通带从 0 Hz 开始，直到达到最大通带增益下降 3 dB 时的谐振频率值。

而对于高通滤波器，通带从 -3 dB 的谐振频率开始，直到有源滤波器的最大环路增益值。低通和高通响应的组合给出了带通响应，如下所示：

有源带通滤波器

根据品质因数，带通滤波器被分为宽带通滤波器和窄带通滤波器。品质因数也被称为“优值”。通过将高通滤波器和低通滤波器级联，并加入一个放大元件，我们可以得到带通滤波器。

放大电路位于高通滤波器和低通滤波器之间，它为这两个滤波器提供隔离，并给出电路的整体电压增益。这两个滤波器的截止频率值必须保持最小差异。

如果这个差异非常小，高通和低通阶段可能会相互作用。因此，为了拥有合适的截止频率水平，放大电路是必要的。

有源带通滤波器的电路图如下所示：

宽带通滤波器

如果品质因数的值小于十，则通带较宽，这为我们提供了较大的带宽。这种带通滤波器被称为宽带通滤波器。

在这种滤波器中，高截止频率必须大于低截止频率。它在设计中使用了两个放大元件（运算放大器）。

首先，信号会通过高通滤波器，该高通滤波器的输出信号趋于无穷大，因此这个趋于无穷大的信号被传递给最终的低通滤波器。

这个低通滤波器将通过高频信号。

当高通滤波器与低通滤波器级联时，我们得到了简单的带通滤波器。为了实现这种滤波器，低通和高通电路的阶数必须相同。

通过将一个一阶低通滤波器与一个高通滤波器级联，我们得到了二阶带通滤波器；而通过将两个一阶低通滤波器与两个高通滤波器级联，形成了四阶带通滤波器。

由于这种级联，电路产生了较低的品质因数值。一阶高通滤波器中的电容将阻断输入信号中的任何直流偏置。

对于二阶滤波器（高 + 低），在两个阻带处的增益滚降为 ±20 dB/十年。高通和低通滤波器必须是一阶的。

同样地，当高通和低通滤波器为二阶时，那么在两个阻带处的增益滚降为 ±40 dB/十年。

带通滤波器的电压增益表达式如下：

$\left| \frac{V_{\text{out}}}{V_{\text{in}}} \right| = \frac{A_{\text{max}} \times (f/f_L)}{\sqrt{\left[1 + (f/f_L)^2\right]\left[1 + (f/f_H)^2\right]}}$

它是由高通和低通滤波器的各自增益得出的，高通和低通滤波器的各自增益如下：

高通滤波器的电压增益：

$\left| \frac{V_{\text{out}}}{V_{\text{in}}} \right| = \frac{A_{\text{max1}} \times (f/f_L)}{\sqrt{1 + (f/f_L)^2}}$

低通滤波器的电压增益：

$\left| \frac{V_{\text{out}}}{V_{\text{in}}} \right| = \frac{A_{\text{max2}}}{\sqrt{1 + (f/f_H)^2}}$

其中 $A_{\text{max}} = A_{\text{max1}} \times A_{\text{max2}}$。

$A_{\text{max1}}$ 是高通阶段的增益， $A_{\text{max2}}$ 是低通阶段的增益。

宽带滤波器的响应如下所示：

窄带通滤波器

如果品质因数的值大于十，则通带较窄，通带的带宽也较小。这种带通滤波器被称为窄带通滤波器。

它只使用一个有源元件（运算放大器），而不是两个，并且这个运算放大器处于反相配置中。在这种滤波器中，运算放大器在中心频率 $f_c$ 处的增益最大。

窄带通滤波器电路

输入信号被施加到反相输入端。这表明运算放大器处于反相配置。这个滤波器电路产生了窄带通滤波器响应。

上述滤波器电路的电压增益为：

$A_V = -\frac{R_2}{R_1}$

滤波器电路的截止频率为：

$f_{c1} = \frac{1}{2\pi R_1 C_1} \quad \text{和} \quad f_{c2} = \frac{1}{2\pi R_2 C_2}$

多反馈有源带通滤波器

这种滤波器电路基于滤波器的负反馈产生一个调谐电路。这种多反馈的重要优势在于，我们可以在不改变中心频率处的最大增益的情况下，改变截止频率的值。这种截止频率的变化可以通过电阻 $R_3$ 来实现。

考虑以下有源滤波器电路，假设改变后的电阻值为 $R_3'$，改变后的截止频率值为 $f_c'$，那么我们可以按以下方式计算新的电阻值：

$R_3' = R_3 \left(\frac{f_c}{f_c'}\right)^2$

这种电路包含两条反馈路径，由于存在多条反馈路径，它也被称为“多反馈带通电路”。这种电路产生一个无穷大增益的多反馈带通滤波器。由于这种电路，品质因数值可以增加到最大 20。

$f_c = \frac{1}{\sqrt{R_1 R_2 C_1 C_2}}$ $Q = \frac{f_c}{\text{带宽}} = \left(\frac{1}{2}\right)\left\{\sqrt{\frac{R_2}{R_1}}\right\}$ $A_{\text{max}} = -\frac{R_2}{2R_1}$ $R_1 = \frac{Q}{2\pi f_c C A_{\text{max}}}$ $R_2 = \frac{Q}{\pi f_c C}$ $R_3 = \frac{Q}{2\pi f_c C(2Q^2 - A_{\text{max}})}$

中心频率处的增益 $A_{\text{max}}$ 必须小于 $2Q^2$，即：

$A_{\text{max}} < 2Q^2$

其中：

• $f_c$ = 截止频率（单位：赫兹）
• $C$ = 电容（ $C_1 = C_2 = C$ ）
• $Q$ = 品质因数
• $A_{\text{max}}$ = 最大增益

有源带通滤波器的频率响应

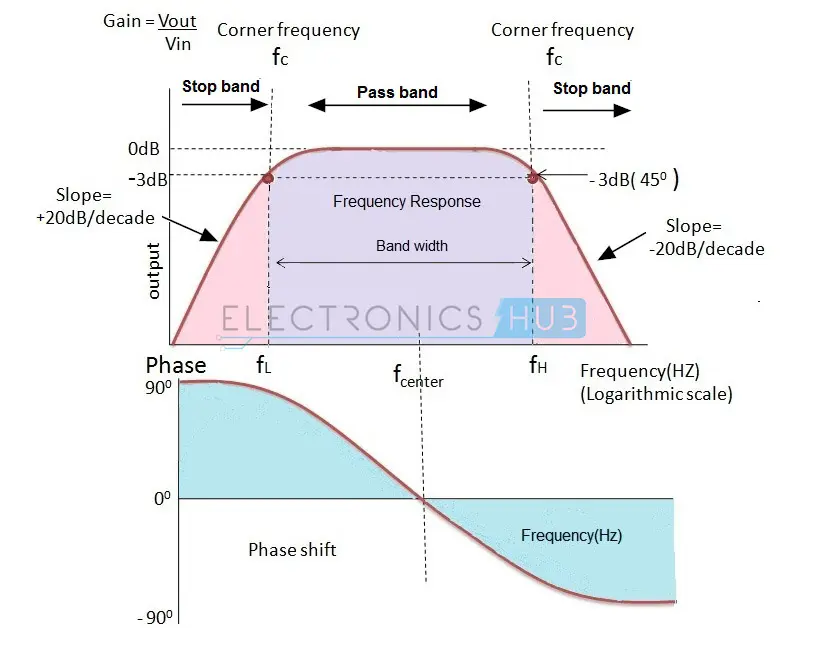
有源带通滤波器的频率响应具有两个中心频率，一个属于高通滤波器，另一个属于低通滤波器。高通滤波器的中心频率必须低于低通滤波器的中心频率。

带通滤波器的中心频率是下截止频率和上截止频率的几何平均值，即：

$f_c = \sqrt{f_L \times f_H}$

滤波器的增益为：

$20 \log \left( \frac{V_{\text{out}}}{V_{\text{in}}} \right) \text{ dB/十年}$

其幅度响应类似于低通和高通滤波器的响应。根据级联滤波器的阶数，响应曲线会有所不同。

假设归一化中频为 $f_r = 1$。假设两个截止频率分别为 300 Hz 和 900 Hz，则滤波器的带宽为 300 Hz 到 900 Hz，即 600 Hz。

品质因数

品质因数取决于通带的带宽。品质因数与带宽成反比。也就是说，如果带宽增加，品质因数会减小；如果带宽减小，品质因数会增加。

$Q = \frac{f_c}{\text{带宽}}$

对于宽带通滤波器，品质因数较低，因为通带宽度较大。对于窄带通滤波器，品质因数较高。选择性和非选择性取决于通带的宽度。

品质因数还与阻尼因子（$\varepsilon$）有关。如果阻尼系数值较大，则输出响应的平坦度也较高。它们之间的关系如下：

$\varepsilon = \frac{2}{Q}$

对于不同的品质因数值，二阶带通滤波器的归一化增益响应如下图所示：

从该图可以看出，品质因数越高，选择性越强。

有源带通滤波器示例

假设一个无穷大增益多反馈有源滤波器电路的谐振频率为 1.5 kHz，最大电压增益为 15，品质因数为 7。则元件值的计算如下：

对于电阻：

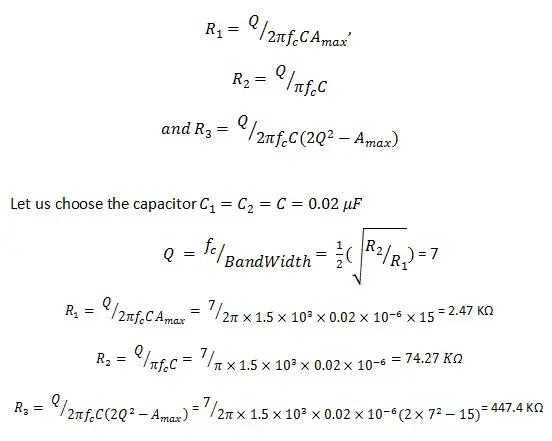
假设改变后的电阻值为 $R_3'$，改变后的截止频率值为 $f_c' = 2$ kHz，则新的电阻值可以按以下方式计算：

$R_3' = R_3 \left( \frac{f_c}{f_c'} \right)^2 = 447.4 \times \left( \frac{1.5}{2} \right)^2 = 251.66 \, \Omega$

因此，通过取所需的频率，我们可以计算出新的电阻值。